Быстрый переход
Блок 1. Вычисления по заданной математической формуле.
Блок 2a. Решение задачи (легкий уровень).
Блок 2b. Решение задачи (средний уровень).
Блок 2c. Решение задачи (повышенный уровень — c вложенными условиями или по реальным ситуациям).
Блок 3. Решение простых задач ОГЭ/ЕГЭ.
Просмотреть справочник простых математических функций
Посмотреть типовые конструкции
Блок 1. Вычисления по заданной математической формуле.
1. Определить значение выражения (2_1_1)
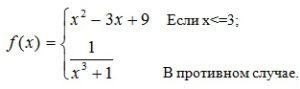
2.Определить значение выражения (2_8_1)
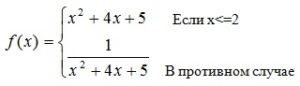
3.Определить значение выражения (2_13_1)
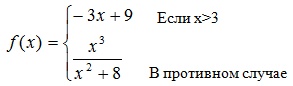
4.Определить значение выражения (2_21_1)
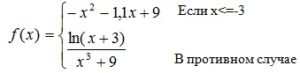
5.Определить значение выражения (2_25_1)

Блок 2a. Решение задачи (легкий уровень).
6.Решить задачу (2_1_2 — «Раздельная обработка»)
Даны три действительные числа. Возвести в квадрат те из них, значения которых неотрицательны, и в четвертую степень – отрицательные.
7. Решить задачу («Максимальное из 2-чисел»)
Вывести на экран максимальное из 2-чисел.
8. Решить задачу («Минимальное из 2-чисел»)
Вывести на экран минимальное из 2-чисел.
9.Решить задачу (Проверка на вхождение в диапазон)
Проверить число на вхождение в диапазон [a,b].
10.Решить задачу (2_10_2 – «проверка на четность и двузначность»)
Проверить число N на чётность и двузначность.
11.Решить задачу (2_11_2 – «равносторонний треугольник»)
Проверить является ли треугольник равносторонним.
12.Решить задачу (2_12_2 – «равнобедренный треугольник»)
Проверить является ли треугольник равнобедренным.
13.Решить задачу (2_13_2 – «противоположные числа»)
Определить, имеется ли среди чисел a, b, c хотя бы одна пара взаимно противоположных чисел.
14.Решить задачу(2_14_2 – «Сколько отрицательных? »)
Подсчитать количество отрицательных чисел среди чисел m, n, p.
Блок 2b. Решение задачи (средний уровень).
15.Решить задачу (2_2_2 – «Ближняя точка плоскости»)
Даны две точки А(x1 , y1), В(x 2, y2). Составить алгоритм, определяющий, которая из точек находится ближе к началу координат.
16.Решить задачу (Найти максимум из 3-чисел)
Определить максимум из 3-чисел.
17.Решить задачу (Найти максимум из 4-чисел)
Определить максимум из 4 — чисел.
18.Решить задачу (Найти минимум из 4-чисел)
Определить минимум из 4 — чисел.
19.Решить задачу (2_1_3 – «max {min (a, b), min (c, d)} »)
Определить max {min (a, b), min (c, d)}.
20.Решить задачу (2_4_2 – «Неожиданное изменение — с двумя вспомогательными переменными»)
Даны действительные числа x и y, не равные друг другу. Меньшее из этих чисел заменить их полусуммой, а большее – их удвоенным произведением.
21.Решить задачу (2_5_2 – «Где на плоскости находится точка»)
На плоскости XOY задана своими координатами точка А. Указать, где она расположена: на какой оси или в каком координатном угле.
22.Решить задачу (2_5_3 – «проверка на упорядоченность»)
Даны действительные числа a, b, c. Удвоить эти числа, если a>=b>=c и заменить их абсолютными значениями, если это не так.
23.Решить задачу (2_6_3 – «точки на числовой прямой»)
На оси ОХ расположены три точки a, b, c. Определить какая из точек b, c расположена ближе к а.
24.Решить задачу (2_7_2 – «сумма цифр со вспомогательными переменными»)
Дано трехзначное число N. Проверить, будет ли сумма его цифр четным числом.
25.Решить задачу (2_7_2b – «сумма цифр без вспомогательных переменных»)
Дано трехзначное число N. Проверить, будет ли сумма его цифр четным числом. (Без вспомогательных переменных).
26.Решить задачу (2_16_3 – «Номер непохожего на другие»)
Известно, что из четырех чисел а1, а2, а3, а4 одно отлично от трех других, равных между собой; присвоить номер этого числа переменной n.
27.Решить задачу (2_18_2 – «Чей делитель? »)
Определить, делителем каких чисел m, n, p является число a.
28.Решить задачу (2_18_3 – «A>B»)
Перераспределить значения переменных х и у так, чтобы в х оказалось большее из этих значений, а в у— меньшее.
Блок 2c. Решение задачи (повышенный уровень — c вложенными условиями или по реальным ситуациям).
29.Решить задачу (2_4_2 – «неожиданное изменение — с одной вспомогательной переменной»)
Даны действительные числа x и y, не равные друг другу. Меньшее из этих чисел заменить их полусуммой, а большее – их удвоенным произведением. Выполнить это задание, только с одной вспомогательной переменной.
30. Решить задачу (2_6_2 – «Замена»)
Даны целые числа m и n. Если числа не равны, то заменить каждое из них одним и тем же числом, равным большему из исходных, а если равны, то заменить числа нулями.
31. Решить задачу (2_2_3 – «Две задачи в одной»)
Даны три числа m, n, p. Определить какое из них равно d. Если ни одно не равно d, то найти max(d-m, d-n, d-p).
32. Решить задачу (2_7_3 – «Треугольник и его площадь»)
Даны три положительных числа a, b, c. Проверить будут ли они сторонами треугольника? Если да, то вычислить площадь этого треугольника.
33. Решить задачу (2_12_3 – «Перевод градусы <-> радианы»)
Cоставить программу, осуществляющую перевод величин из радианной меры в градусную или наоборот. Программа должна запрашивать, какой перевод нужно осуществить, и выполнять указанное действие.
34. Решить задачу (2_14_3 – «Небоскреб»)
В небоскребе бесконечное число этажей и всего один подъезд; на каждом этаже по три квартиры; лифт может останавливаться только на нечетных этажах. Человек садится в лифт и набирает номер нужной ему квартиры N. На какой этаж должен доставить лифт пассажира?
35. Решить задачу (2_19_2 – «Оплата телефона»)
Услуги телефонной сети оплачиваются по следующему правилу: за разговоры за А минут в месяц оплачиваются В р. за минуту , а разговоры сверх установленной нормы оплачиваются из расчета С р. за минуту. Написать программу, вычисляющую плату за пользование телефоном для введенного времени разговоров за месяц D.
36. Решить задачу (2_21_3 – «Квадратное уравнение»)
Если уравнение ах2 + bх + с = 0 (а0) имеет вещественные корни, то решить уравнение и выдать результат, иначе выдать пользователю сообщение «Вещественных корней нет».
37. Решить задачу (2_22_2 – «Грузовик и легковая»)
Грузовой автомобиль выехал из одного города в другой со скоростью v1 км/ч. Через t часов в этом же направлении выехал легковой автомобиль со скоростью v2 км/ч. Составить программу, определяющую, догонит ли легковой автомобиль грузовой через t1 ч после своего выезда.
38. Решить задачу (2_24_2 – «Правильность даты»)
Определить правильность даты, введенной с клавиатуры (число – от 1 до 31, месяц – от 1 до 12). Если введены некорректные данные, то сообщить об этом.
39. Решить задачу (2_25_2 – «Любит — не любит»)
Составить программу, определяющую результат гадания по ромашке – “любит – не любит”, взяв за исходное данное количество лепестков n.
Блок 3. Решение простых задач ОГЭ/ЕГЭ.

